Although there is agreement that the atmosphere is fundamentally
nonlinear, much of low-frequency behavior has been interpreted in
terms of a linear system. A thorough analysis of nonlinear signatures
is often hampered by the data requirements for such a study. With this
issue in mind, an exceptionally long atmospheric general circulation
model (GCM) integration of NCAR's CCM0 is studied to examine the
influence of nonlinearities on low-frequency behavior.
Two approaches reveal nonlinear signatures in projections of the 500-hPa
height field onto phase space planes defined by the leading empirical
orthogonal functions (EOFs):
-
The probability density function (PDF) exhibits departures from a
multivariate normal function, though no more than one maximum is
found (Fig.1).
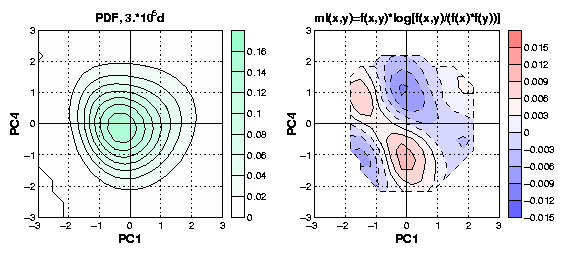 |
Fig.1: a) PDF of the geopotential height in the 2D phase space
spanned by EOF1 and EOF3. b) The mutual information density
f(x,y)*log[f(x,y)/(f(x)*f(y))] emphasizing the density "riges" (with
regard to a bivarite Gaussian) of the PDF in a).
|
-
In some planes the mean phase space velocities (or mean drift)
together with the trajectories they imply produce distinct signatures
of more than one equilibrium point (Fig.2).
 |
Fig.2: Mean trajectory in the 3D-EOF phase space spanned by EOF1, EOF3
and EOF4. The nonlinear tendencies are calculated by removing the
damping component of a least mean square linear fit from the mean
tendencies.
|
With this in mind low-dimensional stochastic models that approximate the
behavior of the GCM in EOF-phase space are built. It turns out that
there is not a unique solution, but that there exists a class of
"stochastically equivalent" models with the same drift and diffusion as
the GCM.
Two models in this class are studied in more detail: one with a linear
deterministic part and multiplicative noise and one with a nonlinear
deterministic part and additive noise. The stationary PDF of these
models agrees remarkably well with the GCM's PDF. Moreover, we show to
what degree even the temporal behavior is captured by the stochastic
models.
We argue that of all low-dimensional stochastic models the most simple
is the model with nonlinear deterministic part and additive white
noise (Fig.3). This model represents the stationary and the temporal behavior
of the GCM geopotential heights in a remarkable manner
 |
Fig.3: a) PDF of of a 2D nonlinear stochastic
model, with nonlinear deterministic part derived from the GCM dataset.
b) The mutual information density
PDF(x,y)/(PDF(x)*PDF(y)) emphasizing the density "riges" (with
regard to a bivarite Gaussian) of the PDF in a).
|
|
![]()
![]()


